Exponential Growth

A variable is said to grow exponentially when its rate of change is proportional to its current value

\[\frac{dV}{dt} = \mu V\]

It is called exponential growth because the variable’s value at any given time (\(t\)) is an exponential function of time \[V_t = V_0 {\rm e}^{\mu t}\]

t <- 1:30
mu <- 0.25
V0 <- 1
Vt <- V0 * exp(mu * t) 
plot(Vt ~ t, type = "l")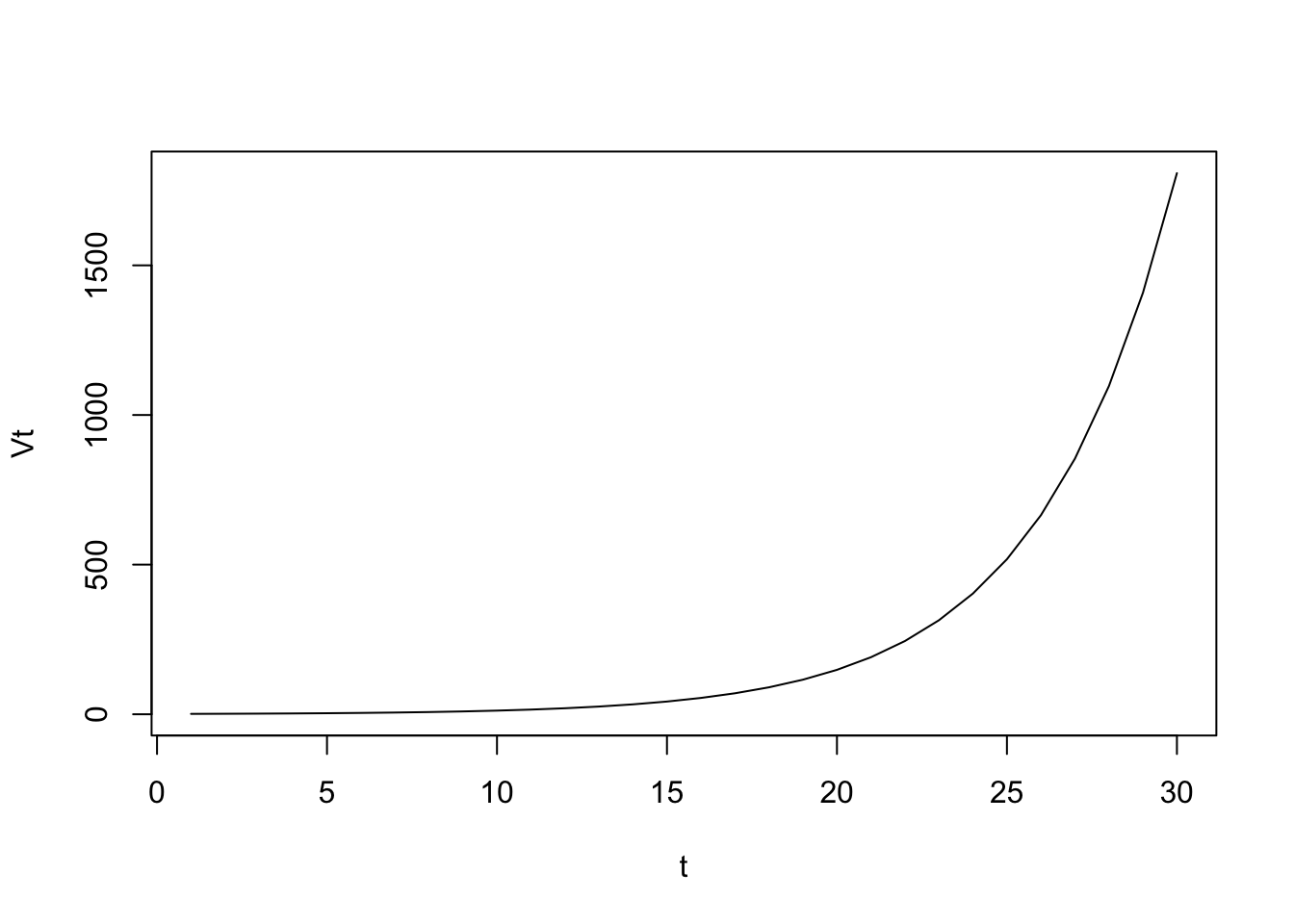

Calculating \(\mu\)

The growth rate \(\mu\) which has units of \(t^{-1}\) is the instantaneous growth rate. It can be calculated from the value of the variable at two different time periods using the equation

\[\mu = \frac{1}{t}\ln\frac{V_t}{V_0}\]

(1/t * log(Vt/V0))[1:2]

## [1] 0.25 0.25

The growth rate can be found from the doubling time (\(t_2\); the number of time intervals required for \(V\) to double) using

\[\mu = \frac{\ln 2}{t_2}\] and from the number of doublings per time interval (\(\delta_t\); a common expression for unicellular organisms) using \[\mu = \delta_t\ln 2\]

It is worth noting that as the exponential term is the product of \(\mu\) and \(t\) it is straightforward to switch between time units. For example to convert a \(\mu\) in units of \(\text{day}^{-1}\) to units of \(\text{hour}^{-1}\) simply divide \(\mu\) by 24.

Negative Exponential Growth

If the growth rate is negative (\(\lambda = - \mu\)) then exponential decay occurs

plot(V0 * exp(-mu * t)  ~ t, type = "l", ylab = "Vt")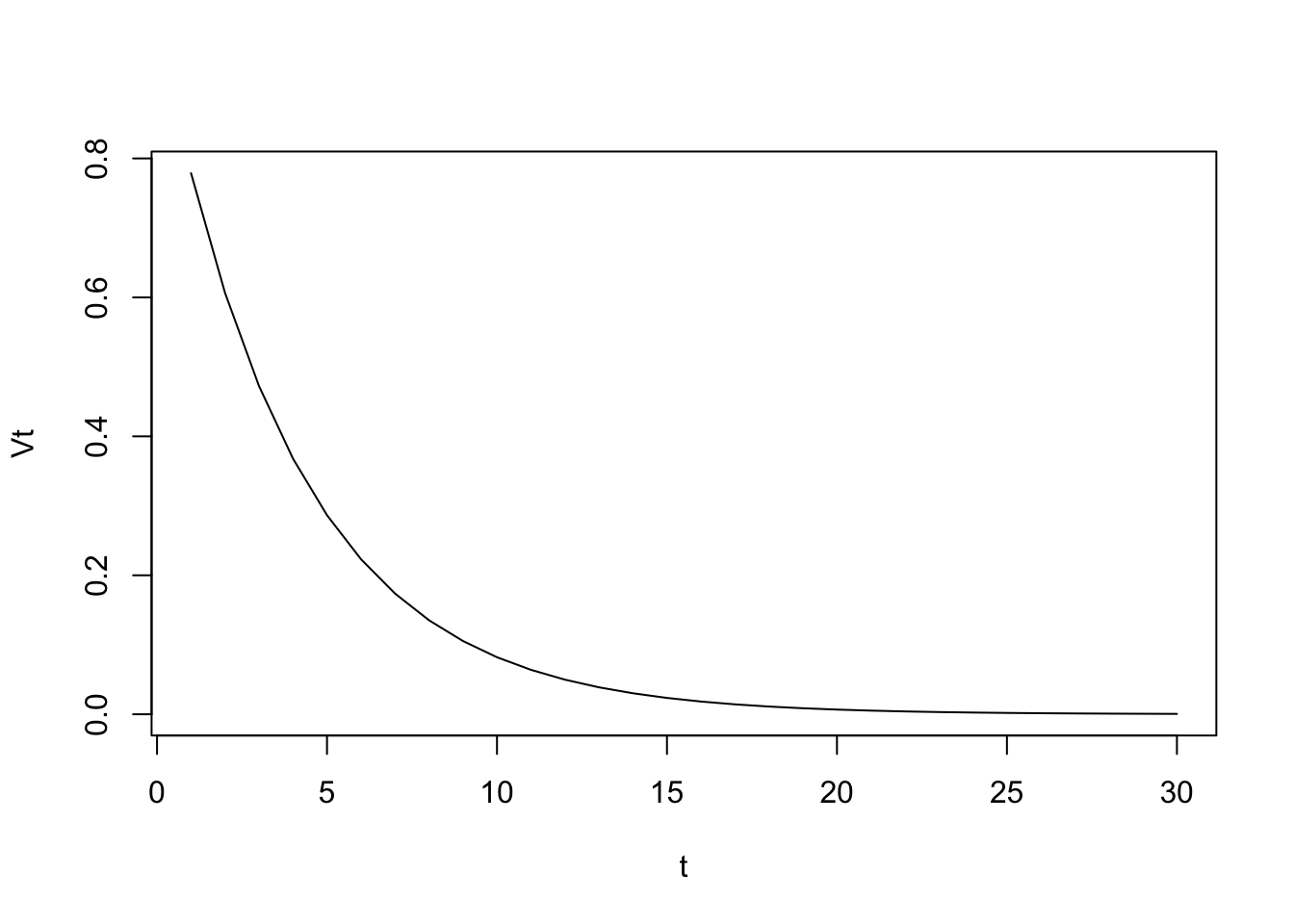

and \(\frac{\ln 2}{\lambda}\) gives the half-life (\(t_{1/2}\)).