Statistical Models

As schematically depicted in Figure 1, statistical inference provides a well-defined pathway from data to uncertainty (in the form of posterior probability distributions).

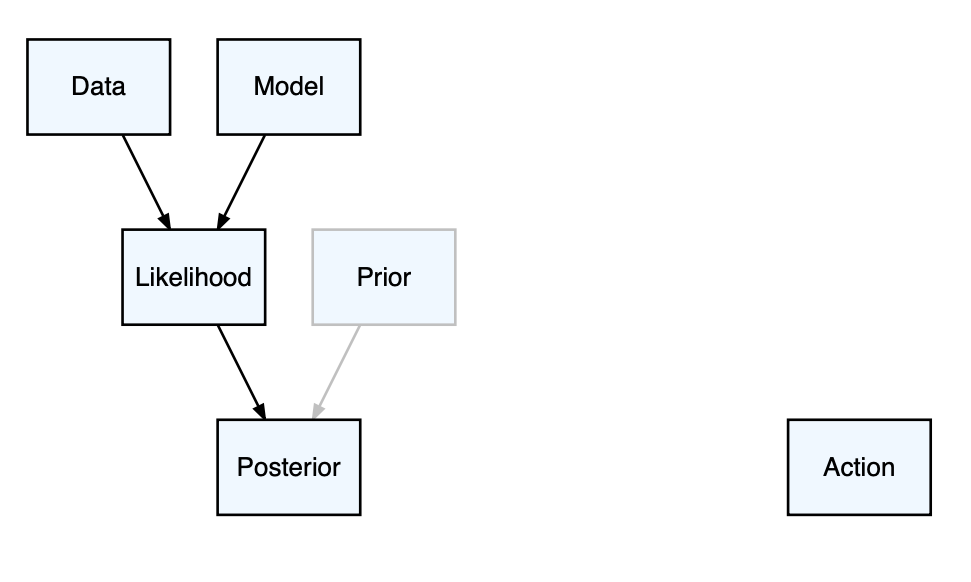
Figure 1. Statistical inference .

The likelihood is the probability of the data given the model parameter values. The posterior probability distributions, which fully capture the uncertainty in the parameter values, are produced by updating any prior information using the likelihood.

Significance

In impact assessments, the most common approach is to convert the posterior probabilities into 95% confidence intervals that are then categorized as being significant if they exclude no effect from the range of possible values. Unless the parameter representing the impact of concern is significant a project is approved. The pathway from uncertainty to action using significance testing is represented in Figure 2.

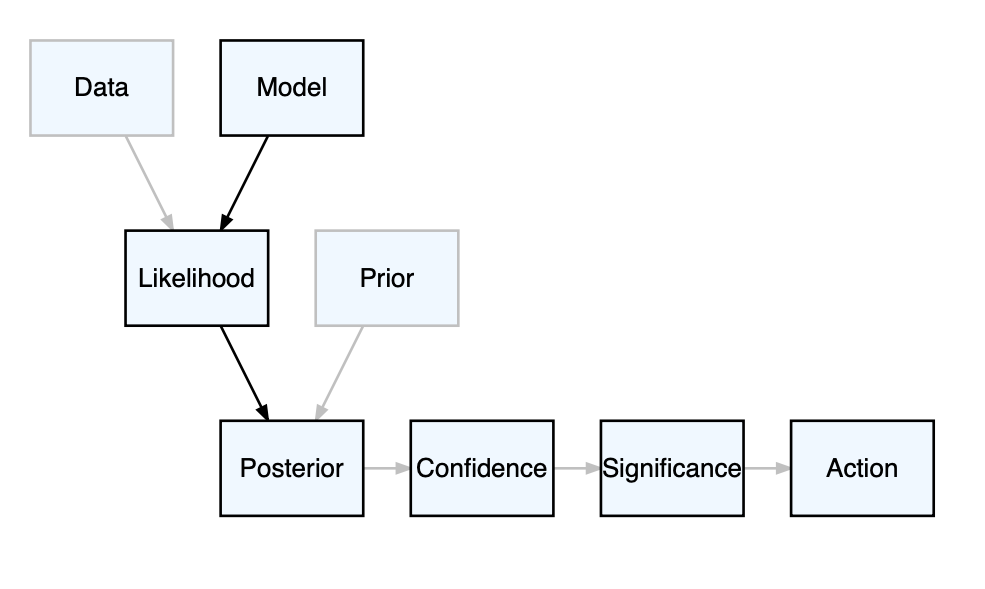
Figure 2. Significance testing. .

The Problem

A problem with significance testing is that substantial uncertainty results in an insignificant result and project approval even if there is a reasonable chance the impact is strongly negative. This violates the precautionary principle and disincentivizes data collection.

Power Analysis

Power analysis calculates the amount of data required to have a reasonable chance of a significant result with an impact above a particular threshold. It enforces data collection.

Prior Information

Incorporation of existing knowledge that an impact is likely to be a particular magnitude, incentivizes data collection if the proponent considers the actual impact to be substantially smaller. Otherwise negative impacts are considered to be as existing knowledge suggests.

Precautionary Principle

The precautionary principle is upheld if a project is not approved unless the estimated effect is significantly less than an acceptable threshold

However significance testing is still a poor framework for decision-making because it ignores most of the information in the posterior probability distribution and doesn’t consider the costs and benefits of the project.

Statistical Decision Theory

Statistical decision theory allows the user to choose the option that maximizes the expected net benefit given the uncertainty. It requires a loss function, which can be challenging to develop, but ensures the criteria used to make a decision are explicit and that the decision is optimal (Figure 3). The loss function represents the relative value of each possible outcome.

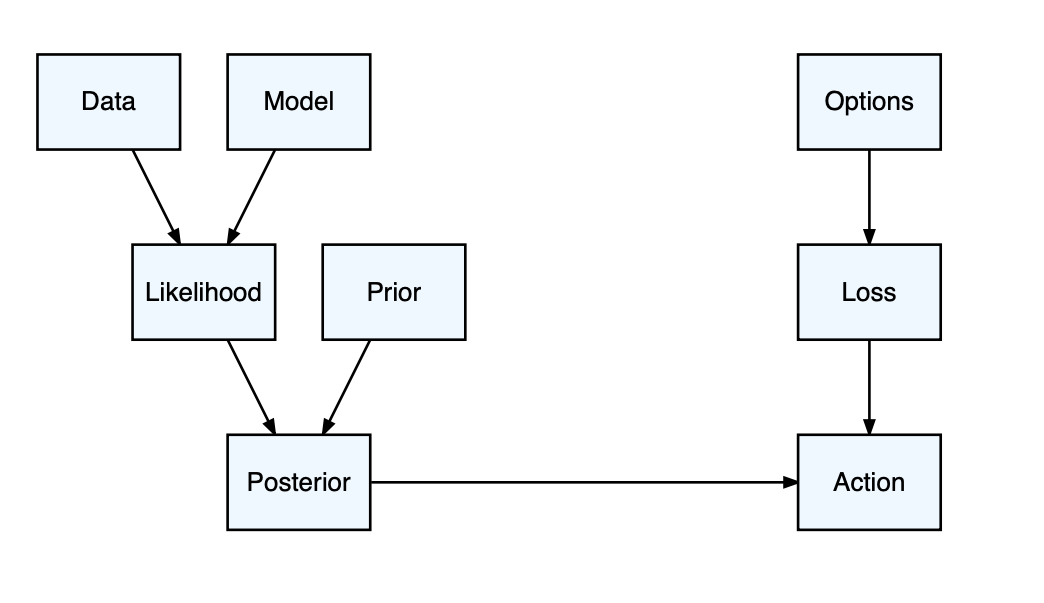
Figure 3. Statistical decision theory. .

Biodiversity Crisis

The UN’s Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services (IPBES) 2019 report warns that as many as 1 million species are now at risk of extinction. If we are to better manage our planet it is essential that we abandon significance as a decision-making tool in environmental impact assessments.